Como Explicar Las Fracciones A Niños De Tercer Grado es una guía integral que brinda a los educadores y padres las herramientas y estrategias necesarias para enseñar este concepto matemático fundamental de manera efectiva. A través de una presentación clara y atractiva, este artículo explora las diferentes formas de representar, comparar y operar con fracciones, al tiempo que destaca sus aplicaciones en la vida cotidiana.
Las fracciones son un concepto esencial en matemáticas que se utiliza para representar partes de un todo. Comprender las fracciones es crucial para desarrollar habilidades matemáticas sólidas y resolver problemas en una amplia gama de situaciones.
Definición de fracciones
Las fracciones son una forma de representar partes de un todo. Se escriben como dos números separados por una barra. El número superior, llamado numerador, indica cuántas partes del todo se tienen. El número inferior, llamado denominador, indica en cuántas partes iguales se ha dividido el todo.
Por ejemplo, la fracción 1/2 representa una mitad, porque el numerador 1 indica que se tiene una parte y el denominador 2 indica que el todo se ha dividido en dos partes iguales.
Representación de fracciones
Las fracciones se pueden representar de diferentes maneras:
- Como números mixtos: Un número mixto es un número entero seguido de una fracción. Por ejemplo, 1 1/2 es un número mixto que representa una parte entera y una mitad.
- Como decimales: Un decimal es un número que tiene una parte entera y una parte decimal. Por ejemplo, 0,5 es un decimal que representa la mitad.
- Como porcentajes: Un porcentaje es un número que representa una parte de un todo por cada 100. Por ejemplo, 50% representa la mitad.
Representación de fracciones
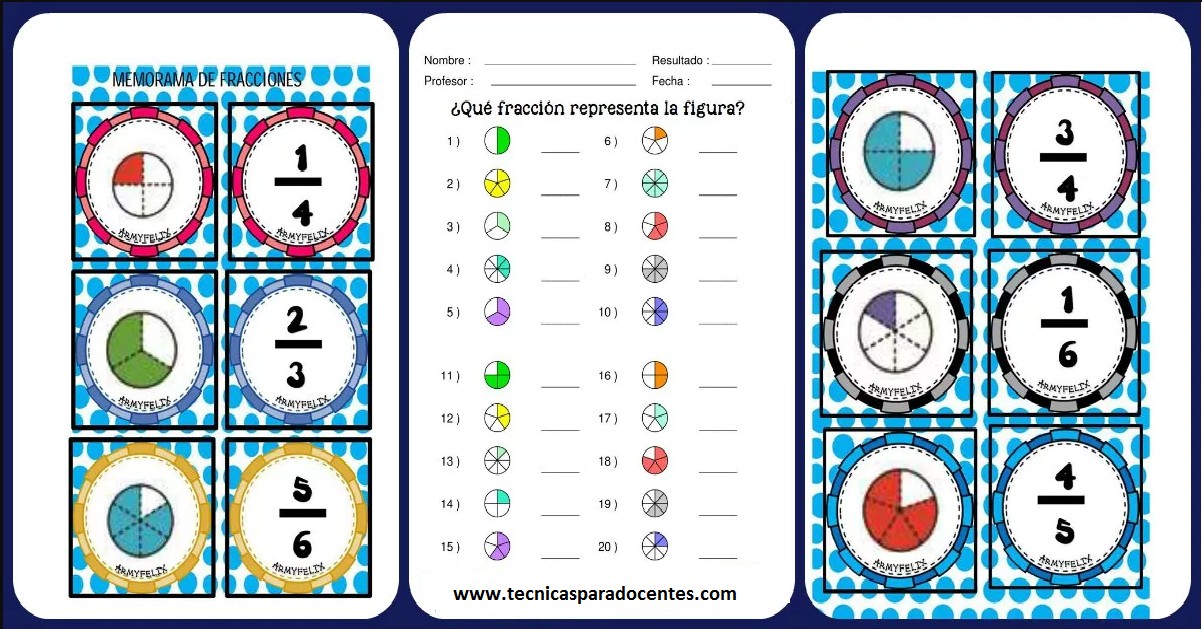
Existen diferentes maneras de representar fracciones, entre las más comunes se encuentran el círculo, el rectángulo y el número mixto.
Representación en círculo
En esta representación, la fracción se muestra como un círculo dividido en partes iguales. El numerador indica el número de partes sombreadas, mientras que el denominador indica el número total de partes.
| Fracción | Representación en círculo |
|---|---|
| 1/2 |  |
| 2/3 |  |
| 3/4 |  |
Representación en rectángulo
Similar al círculo, en esta representación la fracción se muestra como un rectángulo dividido en partes iguales. El numerador indica el número de partes sombreadas, mientras que el denominador indica el número total de partes.
| Fracción | Representación en rectángulo |
|---|---|
| 1/2 |  |
| 2/3 |  |
| 3/4 |  |
Representación como número mixto, Como Explicar Las Fracciones A Niños De Tercer Grado
Un número mixto es una combinación de un número entero y una fracción. Se utiliza cuando el numerador es mayor que el denominador. El número entero representa el número de partes enteras, mientras que la fracción representa la parte restante.
| Fracción | Representación como número mixto |
|---|---|
| 5/2 | 2 1/2 |
| 7/3 | 2 1/3 |
| 10/4 | 2 1/2 |
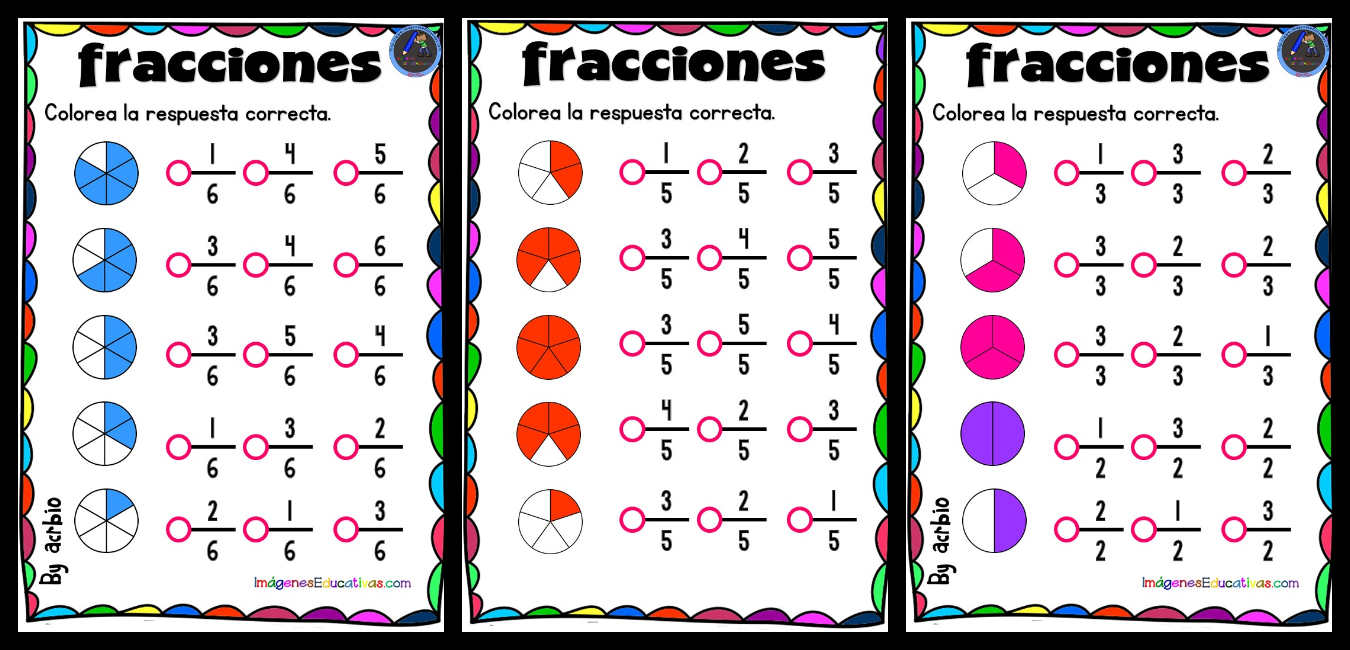
Comparación de fracciones
Comparar fracciones es una habilidad esencial en matemáticas. Nos permite determinar qué fracción es mayor o menor que la otra. En esta sección, exploraremos cómo comparar fracciones con el mismo denominador y con diferentes denominadores.
Comparación de fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, podemos compararlas fácilmente mirando sus numeradores. La fracción con el numerador más grande es la fracción más grande.Por ejemplo:* 1/4 es menor que 3/4 porque 1 es menor que 3.
5/6 es mayor que 2/6 porque 5 es mayor que 2.
Comparación de fracciones con diferentes denominadores
Cuando las fracciones tienen diferentes denominadores, no podemos compararlas directamente. Para compararlas, debemos convertirlas a fracciones equivalentes con el mismo denominador.Una forma de hacerlo es encontrar el mínimo común múltiplo (MCM) de los denominadores. El MCM es el número más pequeño que es divisible por ambos denominadores.Por
ejemplo, el MCM de 4 y 6 es 12. Para convertir 1/4 y 3/6 a fracciones equivalentes con el denominador 12, multiplicamos el numerador y el denominador de cada fracción por el mismo número que hace que el denominador sea 12.* 1/4 = 1
- 3 / 4
- 3 = 3/12
- 3/6 = 3
- 2 / 6
- 2 = 6/12
Ahora que ambas fracciones tienen el mismo denominador, podemos compararlas mirando sus numeradores. En este caso, 6/12 es mayor que 3/12 porque 6 es mayor que 3.
Suma y resta de fracciones
Las fracciones representan partes de un todo y pueden usarse para sumar o restar cantidades. Para sumar o restar fracciones, deben tener el mismo denominador.
Suma de fracciones con el mismo denominador
Para sumar fracciones con el mismo denominador, suma los numeradores y mantén el mismo denominador.
Resta de fracciones con el mismo denominador
Para restar fracciones con el mismo denominador, resta los numeradores y mantén el mismo denominador.
Tabla de ejemplos
| Problema | Solución |
|---|---|
| 1/2 + 1/2 | 2/2 = 1 |
3/4
|
2/4 = 1/2 |
Aplicaciones de las fracciones: Como Explicar Las Fracciones A Niños De Tercer Grado

Las fracciones no son solo conceptos matemáticos abstractos, sino que también tienen aplicaciones prácticas en nuestra vida cotidiana. Desde cocinar y medir hasta jugar y resolver problemas, las fracciones desempeñan un papel importante en varios aspectos de nuestra vida.
En las recetas
Las recetas a menudo requieren ingredientes medidos en fracciones, como 1/2 taza de harina o 1/4 cucharadita de sal. Esto garantiza que los ingredientes se combinen en las proporciones correctas para crear el plato deseado.
En las mediciones
Las fracciones también se utilizan en las mediciones. Por ejemplo, una regla puede estar marcada en fracciones de pulgadas o centímetros, lo que permite mediciones precisas.
En los juegos
Los juegos como las cartas y los dados involucran fracciones. Por ejemplo, en un juego de cartas, las probabilidades de robar una carta específica son una fracción del número total de cartas en la baraja.
“En un juego de damas, el tablero está dividido en 64 cuadrados, cada uno de los cuales representa una fracción del tablero completo. Los jugadores deben mover sus piezas estratégicamente para capturar fracciones del tablero del oponente y ganar el juego”.
En conclusión, Como Explicar Las Fracciones A Niños De Tercer Grado proporciona una hoja de ruta completa para enseñar fracciones a los estudiantes de tercer grado. Al incorporar representaciones visuales, estrategias prácticas y aplicaciones del mundo real, los educadores pueden hacer que el aprendizaje de fracciones sea significativo y atractivo.
Al dominar este concepto fundamental, los estudiantes estarán bien equipados para avanzar en sus estudios matemáticos y desarrollar habilidades esenciales para el éxito en la vida.
